
Boolean algebra
First Class
2016-2017
1
Dr. AMMAR ABDUL-HAMED KHADER

Boolean algebra
Objective
• Understand the relationship between Boolean logic and digital
computer circuits.
• Learn how to design simple logic circuits.
• Understand how digital circuits work together to form complex
computer systems.
2
Dr. AMMAR ABDUL-HAMED KHADER

Boolean algebra
• Mathematician George Boole invented Boolean logic
operations system in 1813 – 1864. Boolean logic is also
known as Boolean algebra. It is a mathematics of digital
systems.
3
Dr. AMMAR ABDUL-HAMED KHADER

Boolean algebra
• Boolean algebra is a mathematical system for the
manipulation of variables that can have one of two
values.
– In formal logic, these values are “true” and “false.”
– In digital systems, these values are “on” and “off,” 1 and 0,
or “high” and “low.”
• Boolean expressions are created by performing
operations on Boolean variables.
– Common Boolean operators include AND, OR, and NOT.
4
Dr. AMMAR ABDUL-HAMED KHADER

Boolean Algebra Operation
•The complement is denoted by a bar . It is defined by
0 = 1 and 1 = 0.
•The Boolean sum, denoted by (+) or by OR, has the following
values:
1 + 1 = 1, 1 + 0 = 1, 0 + 1 = 1, 0 + 0 = 0
•The Boolean product, denoted by () or by AND, has the
following values:
1 1 = 1, 1 0 = 0, 0 1 = 0, 0 0 = 0
5
Dr. AMMAR ABDUL-HAMED KHADER
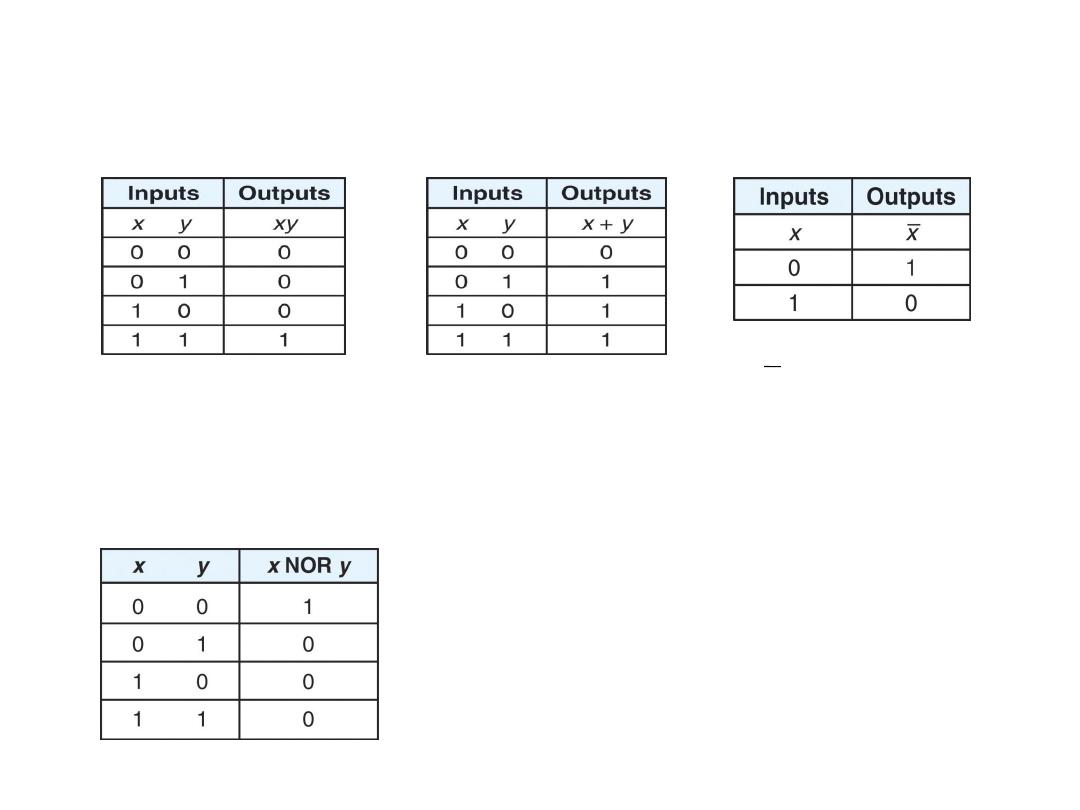
Truth Tables
6
xy = x AND y = x * y
x + y = x OR y
x (bar) = NOT x
AND is true only if
OR is true if either
NOT inverts the bit
both inputs are true
inputs are true
NOR is NOT of OR, NAND is NOT of AND, XOR is true if both inputs differ
Dr. AMMAR ABDUL-HAMED KHADER
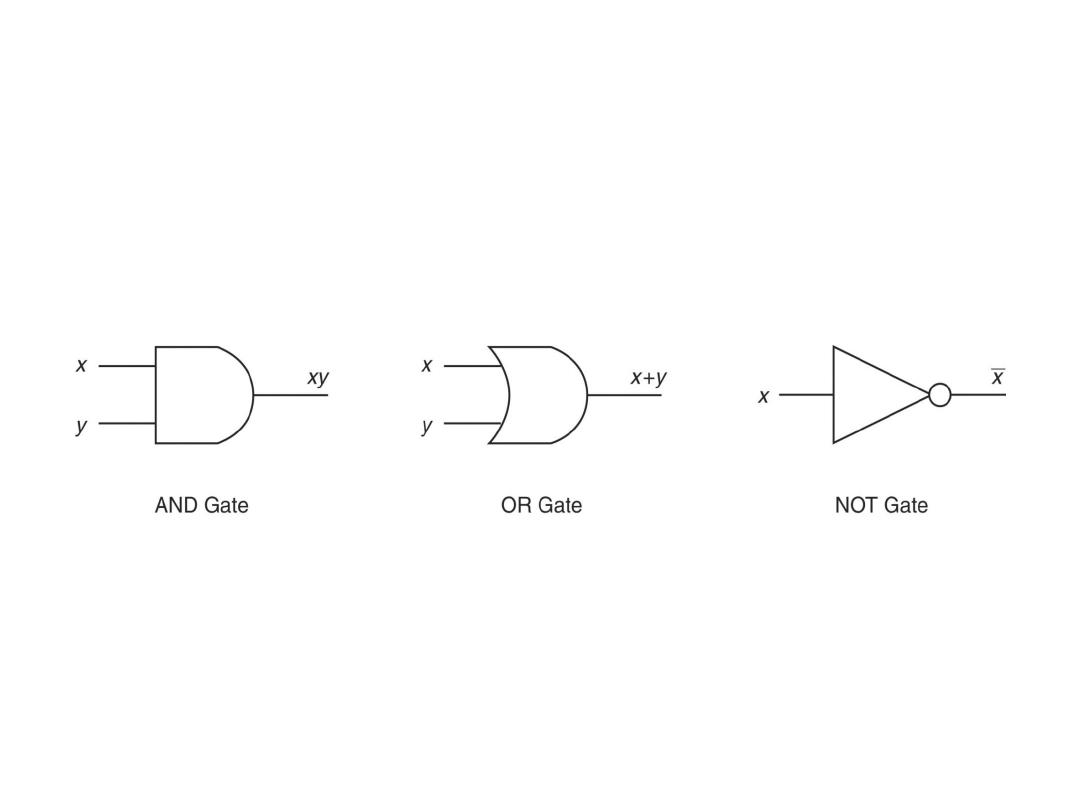
Logic Gates
7
Here we see the logic gates that represent the Boolean operations previously
discussed
-Boolean multiplier -Boolean adder
Dr. AMMAR ABDUL-HAMED KHADER
Switching Circuits
AND
OR

Boolean Addition & Multiplication
• Example 1: Determine the value of A, B, C and D that make
the sum term A + B + C + D equal to 0.
Solution: To gat 0, all the terms should be 0. So A = 0, B = 0,
C = 0, D = 0,
0 + 1 + 0 + 1 = 0.
• Example 2: Determine the value of A, B, C and D that make
the product term A BCD equal to 1.
Solution: To gat 1, all the terms should be 1.
A BCD = 1 . 0 . 1 . 0 = 1
9
Dr. AMMAR ABDUL-HAMED KHADER
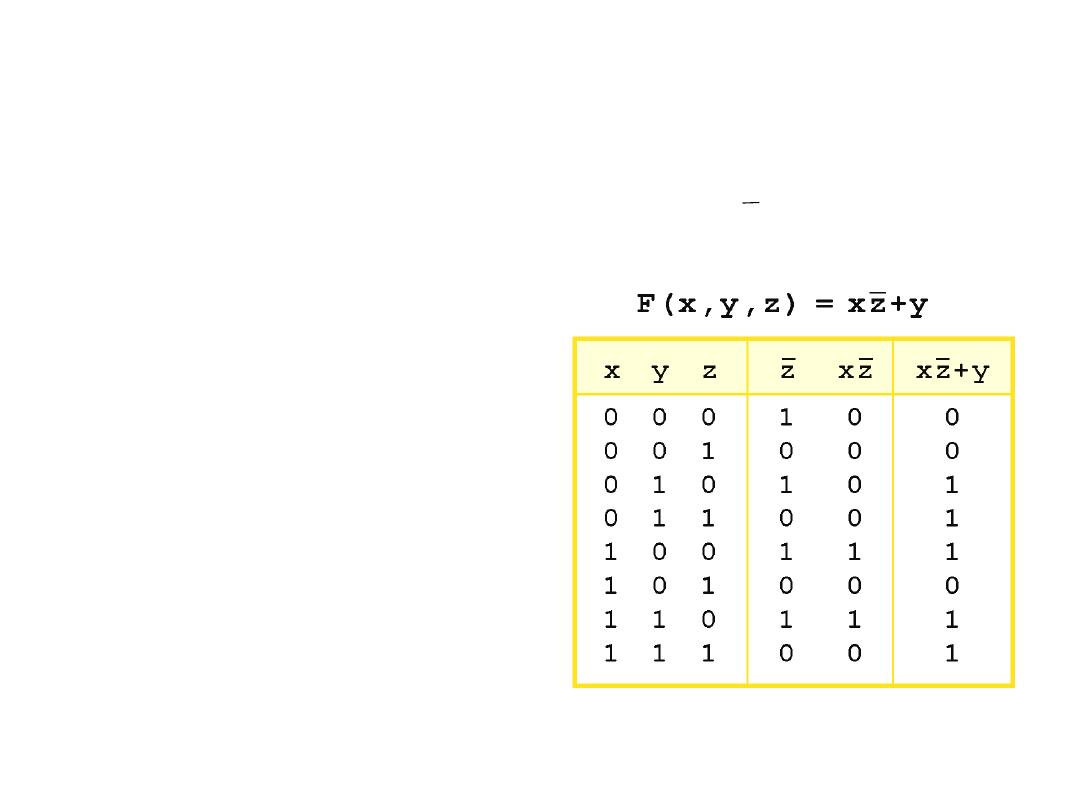
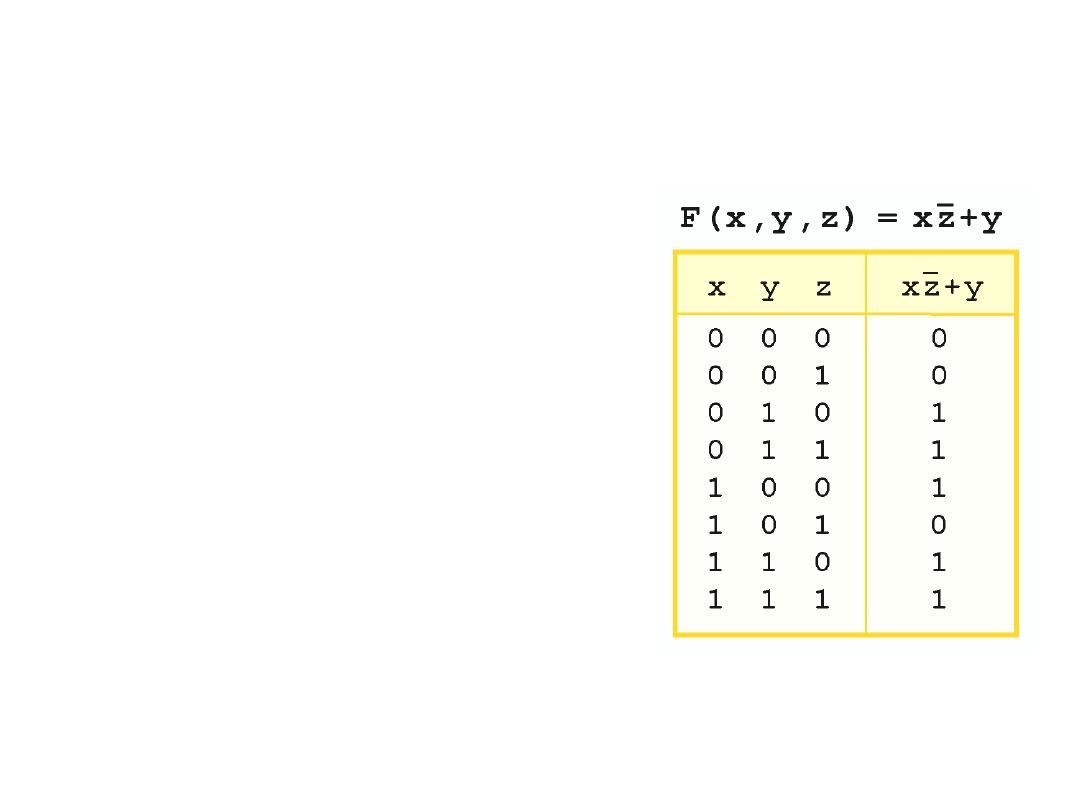
Boolean Addition & Multiplication
• Example: Find the value (F) if F(x,y,z) = xz + y
Solution:
• As with common arithmetic,
Boolean operations have
rules of precedence.
• The NOT operator has
highest priority, followed by
AND and then OR.
• This is how we chose the
(shaded) function subparts in
our table.
10
Dr. AMMAR ABDUL-HAMED KHADER

Boolean Algebra
• Digital computers contain circuits that implement Boolean
functions.
• The simpler that we can make a Boolean function, the smaller
the circuit that will result.
– Simpler circuits are cheaper to build, consume less power, and run
faster than complex circuits.
• With this in mind, we always want to reduce our Boolean
functions to their simplest form.
• So that, there are a number of Boolean identities (rules) that
help us to do this.
11
Dr. AMMAR ABDUL-HAMED KHADER

Simplification of Boolean Functions
An implementation of a Boolean Function requires the use
of logic gates.
A smaller number of gates, with each gate (other then
Inverter) having less number of inputs, may reduce the cost
of the implementation.
There are 2 methods for simplification of Boolean functions.
The algebraic method by using Identities
The graphical method by using Karnaugh Map method
12
Dr. AMMAR ABDUL-HAMED KHADER
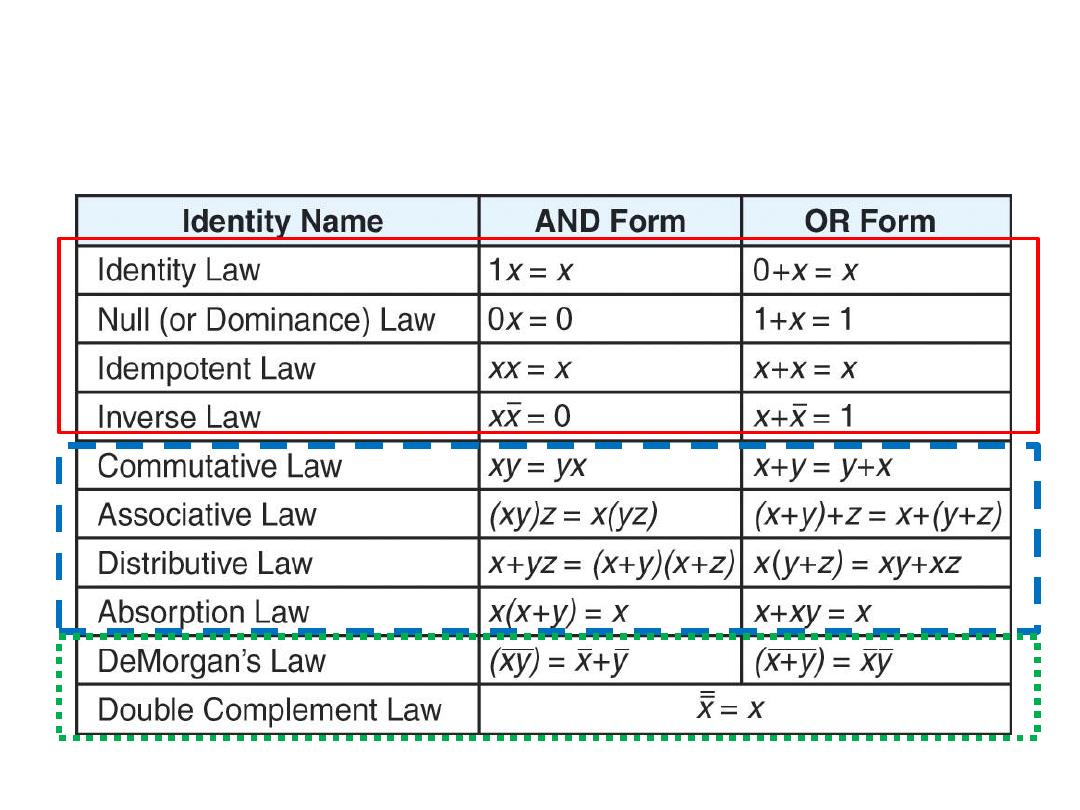
Basic Boolean Identities (Rules)
13
Dr. AMMAR ABDUL-HAMED KHADER

Basic Boolean Identities (Rules)
• Example: simplify using Boolean identities
14
Dr. AMMAR ABDUL-HAMED KHADER
Basic Boolean Identities (Rules)
• Example: xy+xz+yz = xy+xz+yz*1 (identity) =
xy+xz+yz*(x+x) (inverse) =
xy+xz+xyz+xyz (distributive) =
xy(1+z)+xz(y+1) (distributive) =
xy(1)+xz(1) (null) = xy*1+xz*1
(absorption)= xy+ xz (identity)
y
x
z
xy+ xz
15
Dr. AMMAR ABDUL-HAMED KHADER

DeMorgan’s law
• DeMorgan’s law can be extended to any number of variables.
• Replace each variable by its complement and change all ANDs
to ORs and all ORs to ANDs.
• Thus, we find the complement of:
16
Dr. AMMAR ABDUL-HAMED KHADER
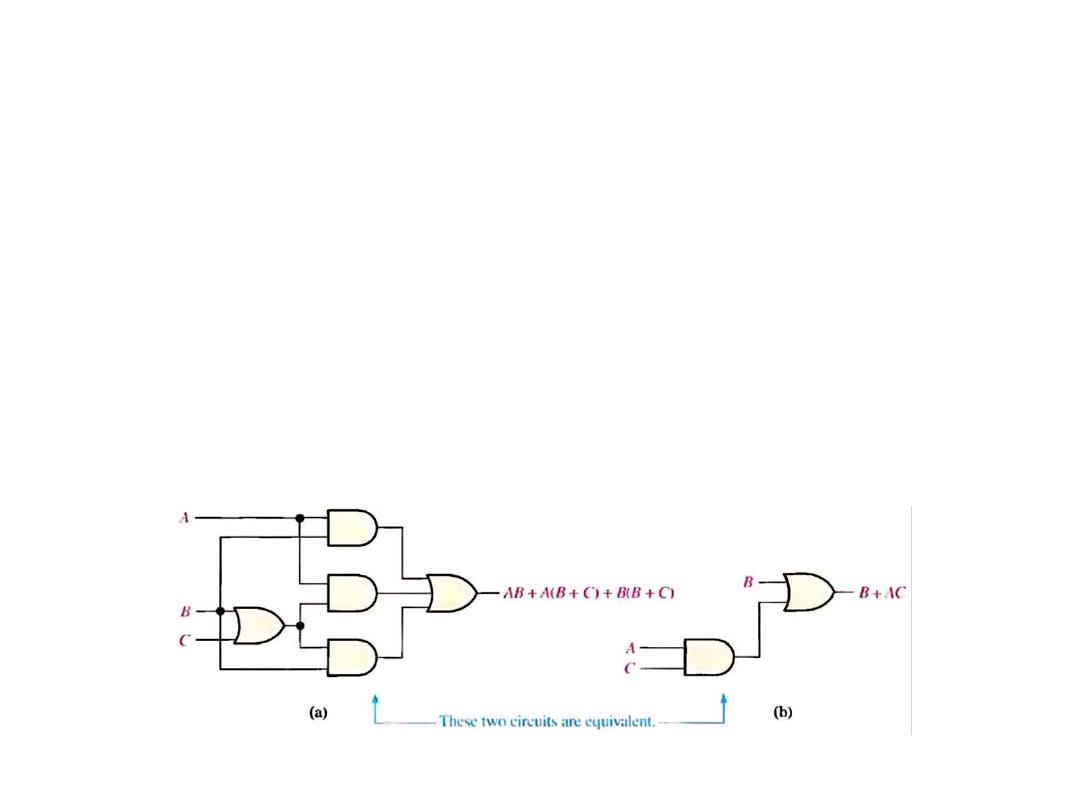
Basic Boolean Identities (Rules)
• Example: simplify using Boolean algebra
AB + A(B+C) + B(B+C)
AB + AB + AC + BB + BC …. (distributed law)
AB + AC + B + BC …. (AB + AB = AB & BB=B)
AB + AC + B ….. (B + BC =B)
B + AC …. (AB + B =B)
17
Dr. AMMAR ABDUL-HAMED KHADER
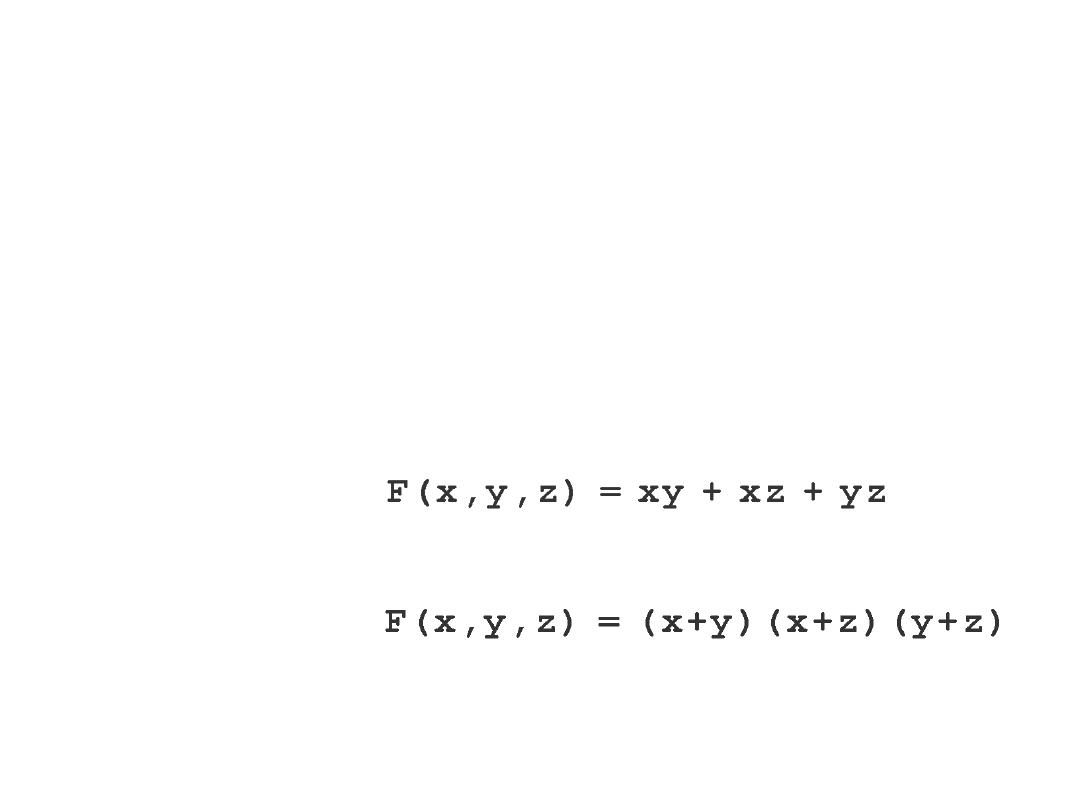
Boolean Algebra
• There are two canonical forms for Boolean expressions: sum-
of-products (SOP) and product-of-sums (POS).
– Recall the Boolean product is the AND operation and the
Boolean sum is the OR operation.
• In the sum-of-products form, ANDed variables are ORed
together.
– For example:
• In the product-of-sums form, ORed variables are ANDed
together:
– For example:
18
Dr. AMMAR ABDUL-HAMED KHADER
Boolean Algebra
• It is easy to convert a function to
sum-of-products form using its
truth table.
• We are interested in the values of
the
variables
that
make
the
function true (=1).
• Using the truth table, we list the
values of the variables that result
in a true function value.
• Each group of variables is then
ORed together.
19
Dr. AMMAR ABDUL-HAMED KHADER

Boolean Algebra
• The sum-of-products form for our
function is:
We note that this function is not in
simplest terms. Our aim is only to
rewrite our function in canonical
sum-of-products form.
20
Dr. AMMAR ABDUL-HAMED KHADER

Boolean Algebra
• Example1: Convert the following Boollean algebra to sum of
product forms: (A + B) + C
Solution: (A + B) + C = (A + B) . C = (A + B) C = AC + BC
• Example2: From the truth table,
determine the standard SOP
expression and the equivalent
standard POS expression
21
Dr. AMMAR ABDUL-HAMED KHADER
Boolean Algebra
• Solution: There are four 1s in the output column and the
corresponding
binary
values
are
011,
100,
110,
111.
Convert these binary values to produce terms as follows:
011
ABC,
100
ABC, 110
ABC, 111
ABC
The resulting standard SOP expression for the output X is
X = ABC + ABC + ABC + ABC
• For the POS expression the output is 0 for the binary values
000, 001 010, 101. Convert these binary values to sum terms:
000
A+B+C, 001
A+B+C, 010
A+B+C, 101
A+B+C
The resulting standard POS expression for the output X is:
X = (A+B+C)(A+B+C)(A+B+C)(A+B+C)
22
Dr. AMMAR ABDUL-HAMED KHADER
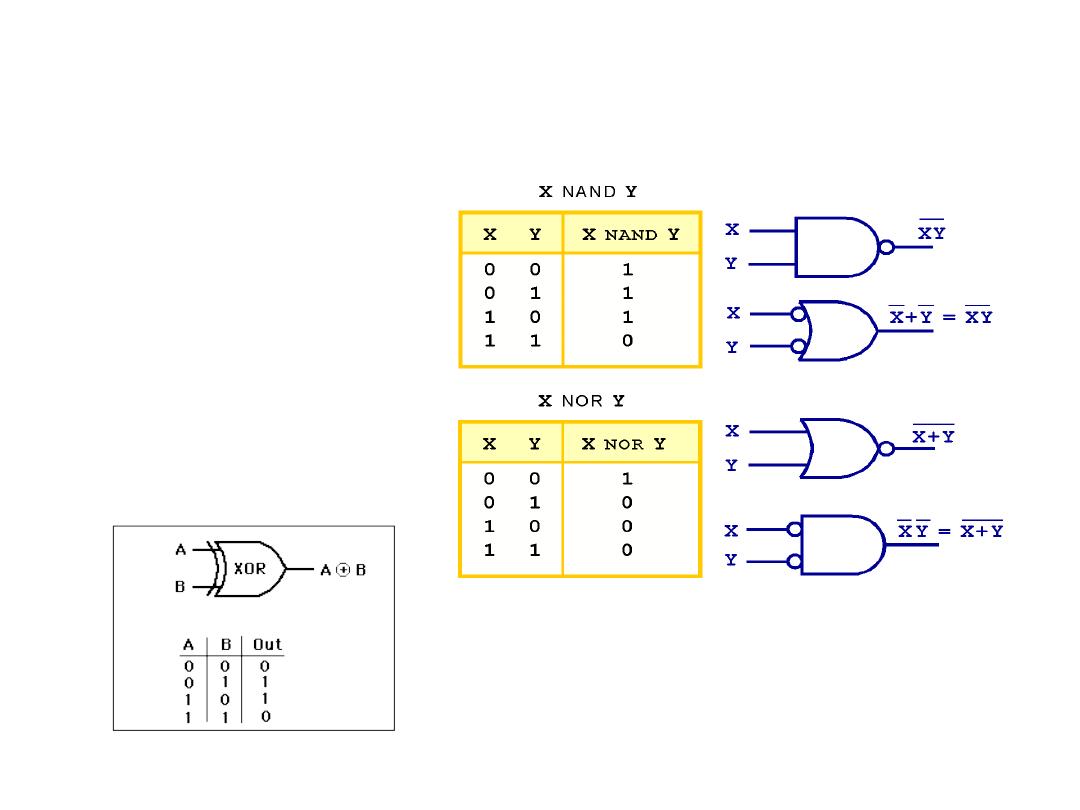
Logic Gates
XOR looks like OR but
with the added curved line
NAND and NOR are
two very important
gates. Their symbols
and truth tables are
shown at the right.
NOR
NAND
23
Dr. AMMAR ABDUL-HAMED KHADER
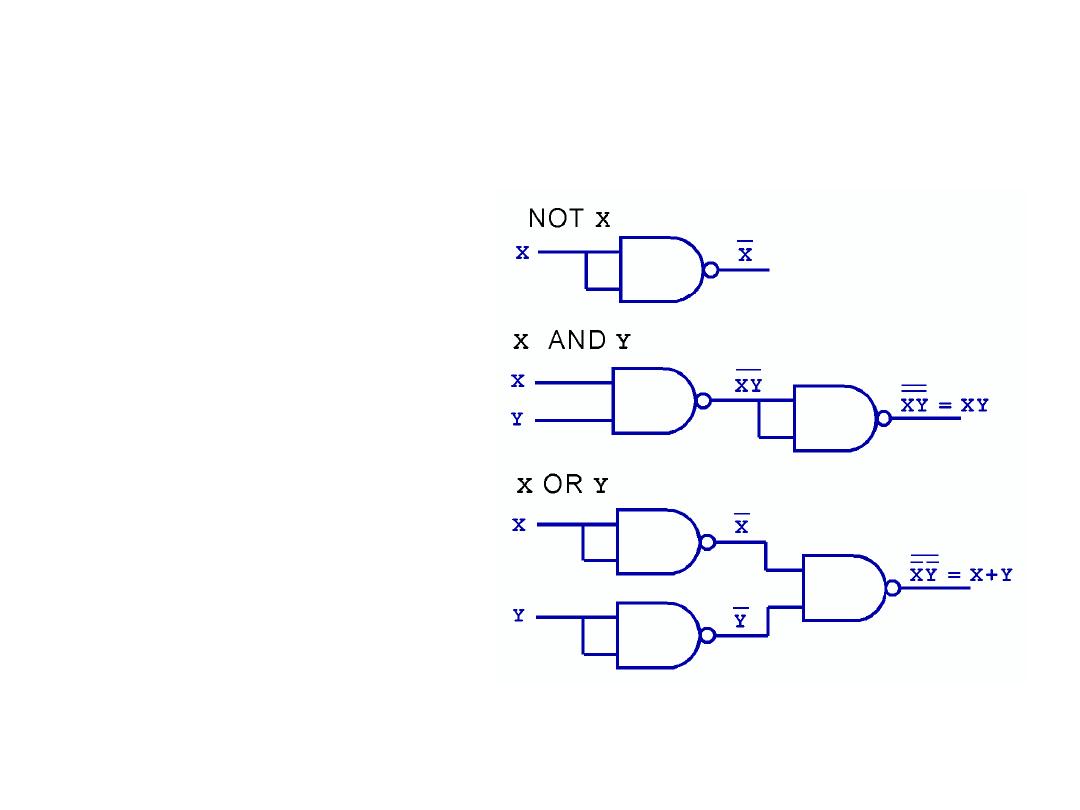
Logic Gates
• NAND and NOR
are known as
universal gates
because they are
inexpensive to
manufacture, and
any Boolean
function can be
constructed using
only NAND or only
NOR gates.
24
Dr. AMMAR ABDUL-HAMED KHADER

Logic Gates
• Fan-in is the number of inputs a gate can handle. Physical
logic gates with a large fan-in tend to be slower than those
with a small fan-in. This is because the complexity of the input
circuitry increases the input
of the device. Using
logic gates with higher fan-in will help reducing the depth of a
logic circuit.
• The fan-out of a
output is the number of gate inputs
it can feed or connect to.
• The maximum fan-out of an output measures its load-driving
capability: it is the greatest number of inputs of gates of the
same type to which the output can be safely connected.
25
Dr. AMMAR ABDUL-HAMED KHADER
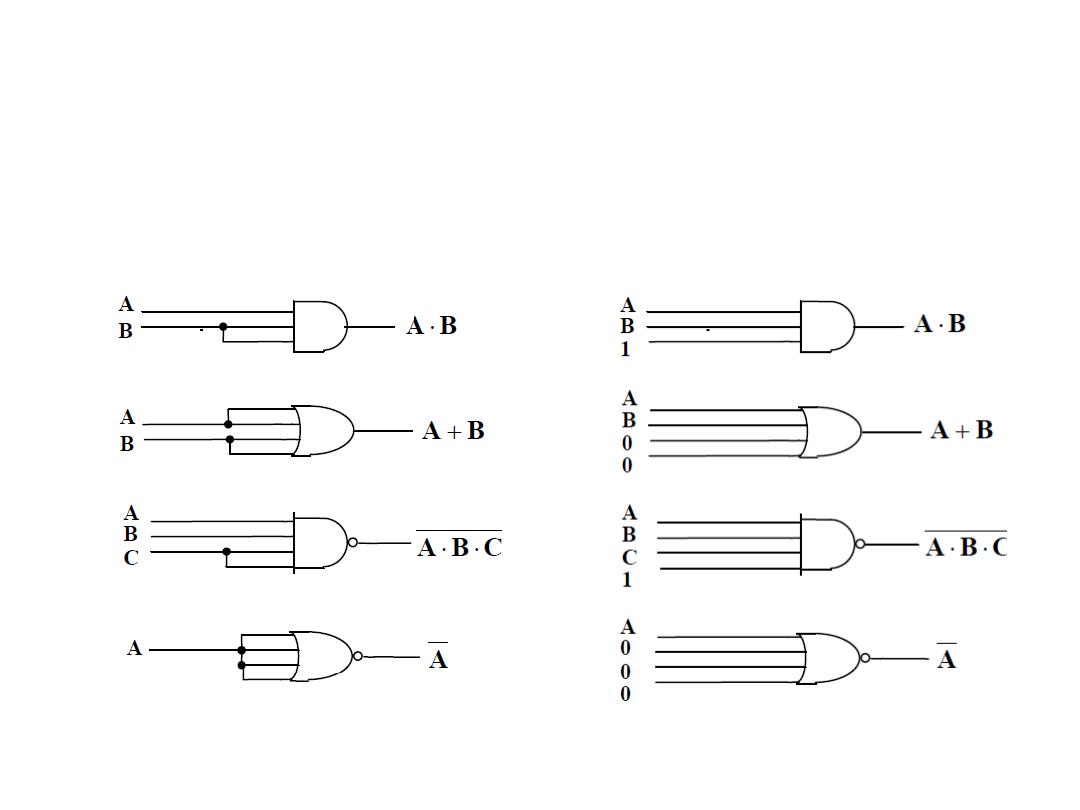
Logic Gates
• To reduce the Fan-in for the gate, we do:
26
Dr. AMMAR ABDUL-HAMED KHADER
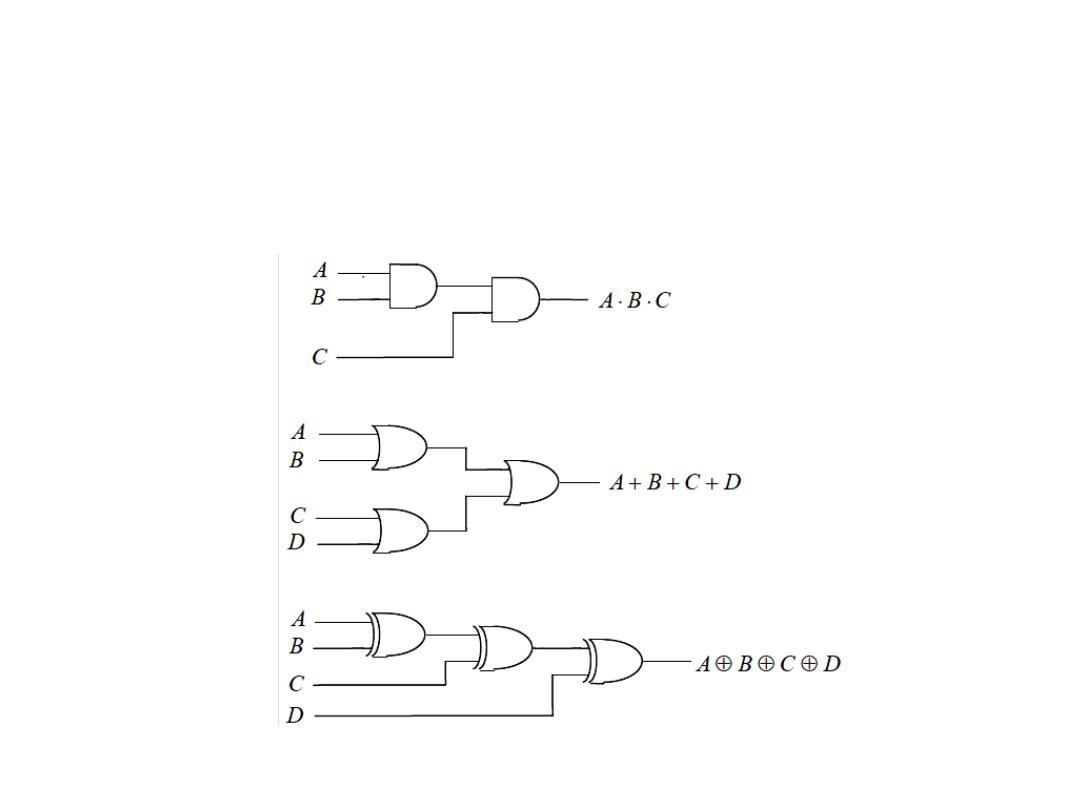
Logic Gates
• If the available gates with limited inputs number, so we do:
27
Dr. AMMAR ABDUL-HAMED KHADER
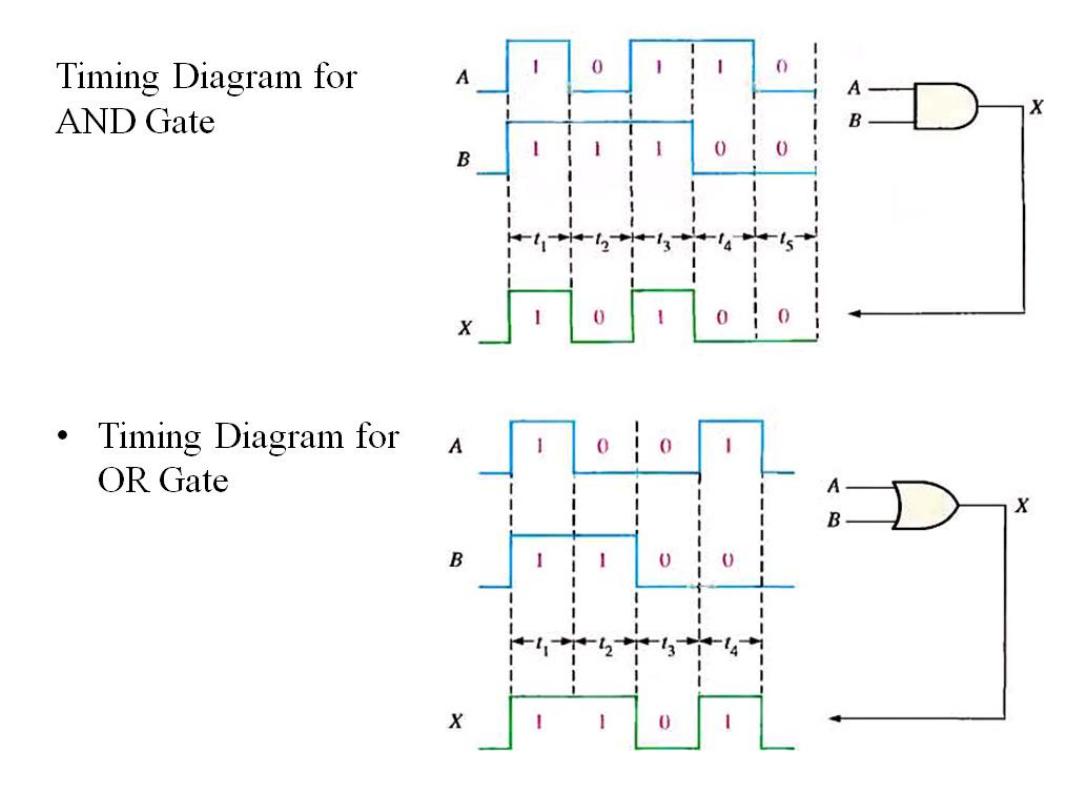
Dr. AMMAR ABDUL-HAMED KHADER
28
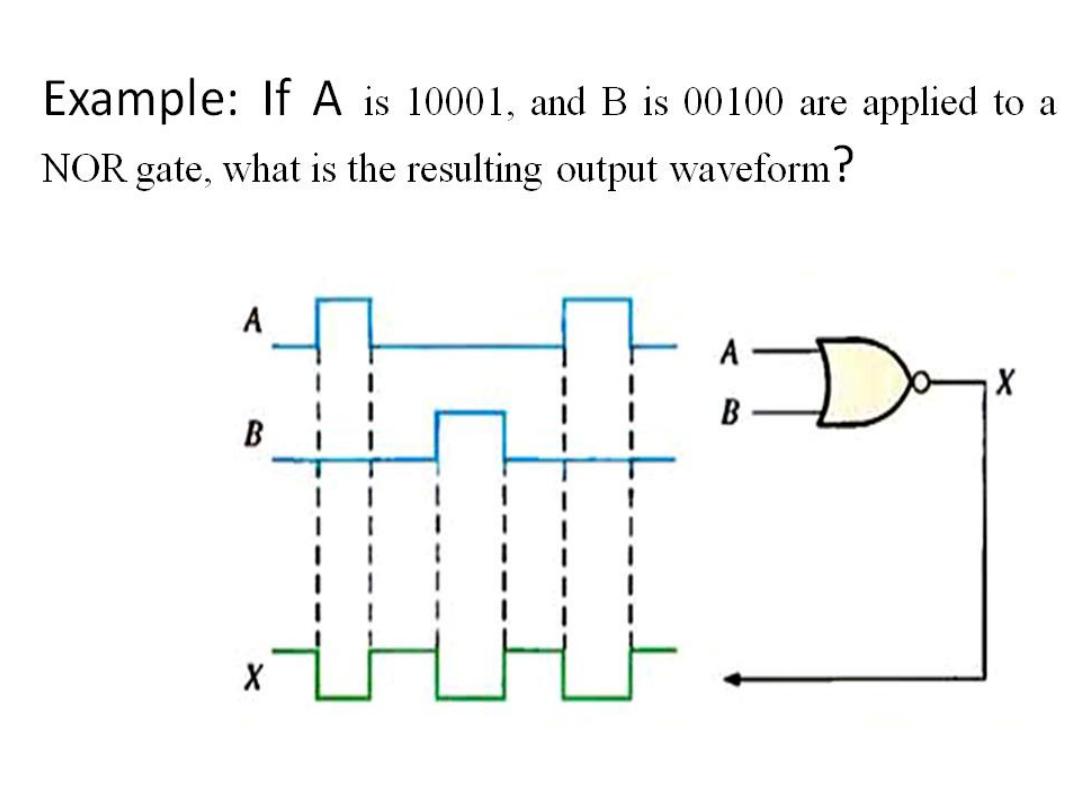
Dr. AMMAR ABDUL-HAMED KHADER
29
